Factor codings for models in R
01 Nov 2015I am holding an exercise on generalised models these days. Preparing a task on factor coding in generalised linear models, I realised that the help on the internet on that is not so easy to understand. At least what I found. So in order to help people who find this topic confusing, I want to help out a little here.
Consider the following data
set.seed(29)
x <- gl(5, 10) # 5 factor's levels, each replicated 10 times
y <- rnorm(n = length(x), mean = as.integer(x), sd = 0.1) # means= 1,2,3,4,5
dd <- data.frame(x = x, y = y)
library(ggplot2)
ggplot(aes(x = x, y = y), data = dd) + geom_boxplot()
means <- tapply(y, x, mean)
means## 1 2 3 4 5
## 0.9962925 2.0227058 3.0230409 3.9482690 5.0189041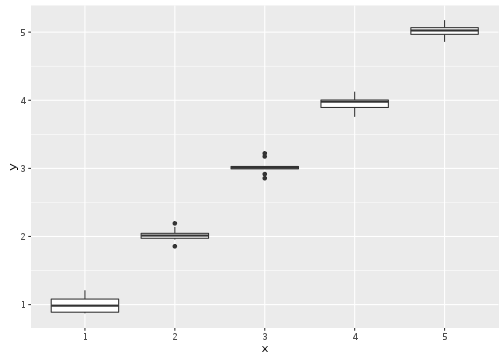
Now we want to model the mean of y given x using the lm() function with the following codings:
dummy-coding, treatment-coding (where the reference category is 5), effect-coding
and split-coding.
To make the theory more general, we have a categorical variable \( X \) with \( K \) categories \( (a_1, \dots, a_K) \)
Dummy-coding
Look at each level separately: \[ E(Y|X=a_{k}) = \beta_k, \quad k=1,\dots,K \]
# dummy (each level singularly)
lm_dummy <- lm( y ~ x - 1, contrasts = list(x = contr.treatment(5)))
summary(lm_dummy)##
## Call:
## lm(formula = y ~ x - 1, contrasts = list(x = contr.treatment(5)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.191692 -0.065303 -0.002686 0.054485 0.214752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## x1 0.99629 0.03293 30.25 <2e-16 ***
## x2 2.02271 0.03293 61.43 <2e-16 ***
## x3 3.02304 0.03293 91.80 <2e-16 ***
## x4 3.94827 0.03293 119.90 <2e-16 ***
## x5 5.01890 0.03293 152.41 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1041 on 45 degrees of freedom
## Multiple R-squared: 0.9991, Adjusted R-squared: 0.999
## F-statistic: 1.014e+04 on 5 and 45 DF, p-value: < 2.2e-16coef(lm_dummy)## x1 x2 x3 x4 x5
## 0.9962925 2.0227058 3.0230409 3.9482690 5.0189041means## 1 2 3 4 5
## 0.9962925 2.0227058 3.0230409 3.9482690 5.0189041Treatment-coding
Compare each category to the dummy-category \( a_d \):
\[ E(Y|X=a_{d}) = \beta_0 \] and \[ E(Y|X=a_k) = \beta_0 + \beta_k, \quad k\neq d \]
# treatment (restrict one level to constant term, all other difference from it)
lm_treatment <- lm( y ~ x, contrast = list(x = contr.treatment(5, base = 5)))
summary(lm_treatment)##
## Call:
## lm(formula = y ~ x, contrasts = list(x = contr.treatment(5, base = 5)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.191692 -0.065303 -0.002686 0.054485 0.214752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.01890 0.03293 152.41 <2e-16 ***
## x1 -4.02261 0.04657 -86.38 <2e-16 ***
## x2 -2.99620 0.04657 -64.34 <2e-16 ***
## x3 -1.99586 0.04657 -42.86 <2e-16 ***
## x4 -1.07064 0.04657 -22.99 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1041 on 45 degrees of freedom
## Multiple R-squared: 0.9951, Adjusted R-squared: 0.9947
## F-statistic: 2293 on 4 and 45 DF, p-value: < 2.2e-16coef(lm_treatment)## (Intercept) x1 x2 x3 x4
## 5.018904 -4.022612 -2.996198 -1.995863 -1.070635c(means[5], means[1:4] - means[5]) ## 5 1 2 3 4
## 5.018904 -4.022612 -2.996198 -1.995863 -1.070635Effect-coding
Compare each category to the mean:
\[ E(Y|X=a_k) = \beta_0 + \beta_k, \quad k=1,\dots,K-1 \] and \[ E(Y|X=a_K) = \beta_0 - \sum\limits_{j=1}^{K-1} \beta_j \]
# effect(deviation from overall average)
lm_effect <- lm(y ~ x, contrast = list(x = contr.sum(5)))
summary(lm_effect)##
## Call:
## lm(formula = y ~ x, contrasts = list(x = contr.sum(5)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.191692 -0.065303 -0.002686 0.054485 0.214752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.00184 0.01473 203.84 <2e-16 ***
## x1 -2.00555 0.02945 -68.09 <2e-16 ***
## x2 -0.97914 0.02945 -33.24 <2e-16 ***
## x3 0.02120 0.02945 0.72 0.475
## x4 0.94643 0.02945 32.13 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1041 on 45 degrees of freedom
## Multiple R-squared: 0.9951, Adjusted R-squared: 0.9947
## F-statistic: 2293 on 4 and 45 DF, p-value: < 2.2e-16coef(lm_effect)## (Intercept) x1 x2 x3 x4
## 3.00184245 -2.00554992 -0.97913668 0.02119841 0.94642653c(mean(means), means[1:4] - mean(means))## 1 2 3 4
## 3.00184245 -2.00554992 -0.97913668 0.02119841 0.94642653Split-coding
Compare each category to the previous category (for ordered categories):
\[ E(Y|X=a_1) = \beta_0 \] and \[ E(Y|X=a_k) = \beta_0 + \sum\limits_{j=1}^{k-1} \beta_j, \quad k=2,\dots,K \]
# split coding
c <- rbind( c(0,0,0,0),
c(1,0,0,0),
c(1,1,0,0),
c(1,1,1,0),
c(1,1,1,1) )
lm_split <- lm(y ~ x, contrast = list(x = c))
summary(lm_split)##
## Call:
## lm(formula = y ~ x, contrasts = list(x = c))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.191692 -0.065303 -0.002686 0.054485 0.214752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.99629 0.03293 30.25 <2e-16 ***
## x1 1.02641 0.04657 22.04 <2e-16 ***
## x2 1.00034 0.04657 21.48 <2e-16 ***
## x3 0.92523 0.04657 19.87 <2e-16 ***
## x4 1.07064 0.04657 22.99 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1041 on 45 degrees of freedom
## Multiple R-squared: 0.9951, Adjusted R-squared: 0.9947
## F-statistic: 2293 on 4 and 45 DF, p-value: < 2.2e-16coef(lm_split)## (Intercept) x1 x2 x3 x4
## 0.9962925 1.0264132 1.0003351 0.9252281 1.0706351c(means[1], diff(means))## 1 2 3 4 5
## 0.9962925 1.0264132 1.0003351 0.9252281 1.0706351